中学受験算数の図形問題には補助線が決め手?灘中の場合
2017年も東大の合格発表が終わり、
開成が連続して東大合格者数では
日本一を達成しました。
最難関の東大理科三類への合格者数で見ると、
兵庫の灘高校の出身者が高い合格率と
多くの合格者を排出しています。
最難関の灘へ入学するには、
灘中への中学受験を制覇する必要があります。
2017年で出題された灘中算数の図形問題も
簡単そうに見えて、
補助線などの一工夫が必要な問題が出題されています。
2017年灘中 中学受験の算数の図形の問題は簡単そうで難しい?
2017灘中 算数
灘中の算数の図形問題で出題された大問の
(1)のとっかかりの部分の問題です。
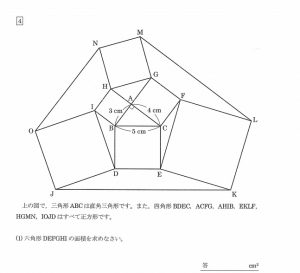
画像にしめすような六角形DEFGHIの面積を求める問題です。
(解法を理解する必要はありません。何が求められているのかだけ、
理解していただければということで説明していきます)
六角形DEFGHI=正方形AHIC+正方形BCED+正方形ACFC+三角形ABC
三角形BID+三角形CEF
でもとめることができます。
正方形AHIC+正方形BCED+正方形ACFC+三角形ABCについては、
順番に、
9、25、16、6(平方センチメートル)
であることは明らかです。
簡単そうに見えるのですが、
残りの
三角形BIDと三角形CEFの面積はどのように計算したらいいのでしょうか?
三角形BIDの場合には、BDの長さが5センチということがわかっています。
このBDをこの三角形の底辺と考えられるなら、
高さがわかるなら
三角形の面積の公式に当てはめれば答えが出ます。
つまり、点Iから辺BDに下ろした垂線(垂直におろした線)
の長さがわかれば求められます。
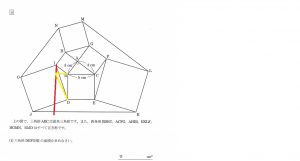
解法の1つは補助線を引く
BDに平行な線を点Iから引いた線が
上図の「赤い線」です。
(画像をクリックすると大きく見えます)
赤い線上を点Iがどこに動こうとも、
三角形BIDの面積は変わりません。
(なぜなら、高さが変わらないから)
なら、点Iを赤い補助線上で
角IBDが直角になるような直角三角形を
つくってみてください。
(上の画像では、黄色い線で書いてあります)
すると、黄色い直角三角形は
直角三角形ABCと相似であることに気が付きますので、
点Iから辺BCまで下ろした垂線の長さは、
3✕(5分の4)=5分の12
と計算できます。
したがって、
三角形BIDの面積は
5✕(5分の12)÷2=6と計算できます。
三角形CEFについても、
辺CEを底辺と考えて、同じように補助線をひいてみると、
面積は同じ6平方cmと計算できます。
六角形DEFGHIの面積は74平方センチメートルと
計算できます。
ポイントは平行線と直角三角形の相似の活用を補助線をひいて考えること
中学受験の算数の図形問題はそのまま眺めていても
解けない場合があることがわかります。
典型的な問題ではなく、
わりと珍しいタイプの問題です。
しかし、活用するのは、
平行線という補助線をひいたりするというのは、
多くの中学受験の算数図形問題では
行われている作業です。
三角形の面積は、底辺を固定して、
もう一つの点を底辺に平行な線上を移動しても、
面積は不変だという基本的な知識を活用し
補助線を引いて問題が解決する良問ですね。
直角三角形の相似を活用すれば、
比率で、高さが計算できるはずという
先行きの見通しをたてられるかも
大切な点でしょう。
補助線を引くと解決できる図形問題にはパターン化されたものも
ありますけれども、
あのパターンと同じというような問題でない点が
灘中らしいですね。
灘中、開成中学レベルのハイレベル図形問題に対応するには?
灘中と開成中学は、東大の合格者数や合格率でトップの座を争う
超難関校です。
平面図形の問題でも標準的な問題からひとひねり、
工夫がされています。
予習シリーズなどの教材で基本ができていれば、
問題ないという天才肌の小学生もいるかもしれませんけれども、
一般的には通塾での訓練が必要です。
それも、受験全解のような市販の教材、
塾専用の教材を外部から購入するような塾、
または、中学受験の過去問のコピーでテキストを作成するような
塾では合格はできないです。
塾講師が灘中、開成中学レベルのハイレベルな問題を作問できるような
力量をもつ塾講師がいるか、
オリジナル教材を作成する部署に優れた人材がいなければ、
合格は難しいのが実情です。
裏を返せば、通塾している塾が灘や開成などの難関校への実績がないなら、
合格するためには、作問脳力には定評があるZ会などを活用して、
独学での努力が必要になります。
Z会の通信教育 資料請求 ![]() をしてみると、
をしてみると、
開成中学へ「通塾無しで、Z会だけで合格した」Iさん(資料には実名と写真があります)
が掲載されていました。
Z会だけで開成中学へ合格するなど
普通は信じられない偉業です。
合格者は特定の塾で競争心をあおられながら、
合格へむけての訓練を受けてます。
通塾先でもっと、開成対策を充実させて欲しい、
もっともっと、難問を解いてみたいという知的好奇心が高い小学生なら
Z会を活用して灘や開成へ合格できる
ということなのでしょう。
もちろん、いまのところ、御三家中学への合格は
特定の実績がある塾へ通塾するのが基本ではあります。
時間を節約して、遊びと学びの時間を充実させて、
睡眠時間もしっかりと確保したいという動機で、
Z会に入会したと、開成中学へ合格したIさんは、
体験を述べています。
頭脳をフル回転させるためには、睡眠時間を重視して、
受験勉強をすすめるというスタイルは理想です。
塾では大量の教材やプリントが配布され、
塾での学習時間も膨大ですし、
家庭学習も自分のペースではなく
塾が提供したボリュームをこなしていく必要があります。
自学自習できる人は、中学への算数と
Z会 小学生向け講座 ![]() があれば十分なのかもしれません。
があれば十分なのかもしれません。
図形や補助線についての本
暇つぶしに肩の力を抜いて読んでみたいのが 中学受験を
題材にした補助線の引き方をテーマにした本です。
- なんでそんな補助線を引くのか、
- 補助線の引き方がうまいと考察力があるといえるのか、
そのあたりは疑問に思うこともありますけれども、
受験算数を解き明かす決め手になる
補助線についての参考図書として
目を通しておいても良いかもしれません。
また、灘中合格実績日本一の浜学園で活躍した前田昌宏先生が
書いた本としては、
は
難関校の受験問題に最適!特に必要な問題が抜粋されてて難問解消に役立ちました。
というAmazonのレビューもあります。